Παρουσίαση/Προβολή
Υπολογιστική Πολυπλοκότητα
(M171 και ΘΠ20) - Αρχοντία Γιαννοπούλου
Περιγραφή Μαθήματος
Στόχος του μαθήματος είναι ο αυστηρός ορισμός της χρονικής και χωρικής πολυπλοκότητας των αλγορίθμων, ο ορισμός των βασικών κλάσεων πολυπλοκότητας και η παρουσίαση αντιπροσωπευτικών προβλημάτων για κάθε μία από αυτές.
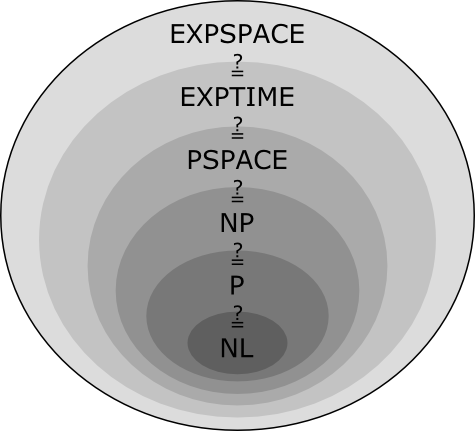
Μεγάλη έμφαση δίνεται στην περιγραφή του μη-ντετερμινιστικού υπολογισμού και στην παρουσίαση του ερωτήματος αν οι κλάσεις P και NP ταυτίζονται.
Τέλος, επιδιώκεται η εξοικείωση των φοιτητών με τις τεχνικές κατάταξης προβλημάτων στις κλάσεις πολυπλοκότητα.
(Περισσότερες πληροφορίες εδώ.)
Ώρες διδασκαλίας:
Τετάρτη 15:00 - 17:00 στην Αίθουσα Z.
Παρασκευή 10:00 - 12:00 στην Αίθουσα Ε.
Ημερομηνία δημιουργίας
Δευτέρα 1 Οκτωβρίου 2018
-
Περιεχόμενο μαθήματος
Υπολογισιμότητα:
- Μηχανές Turing (πολυταινιακές Μ.Τ., μη-ντετερμινιστικές Μ.Τ.)
- Η θέση Church-Turing.
Χρονική πολυπλοκότητα:
- Σχέση πολυπλοκότητας μεταξύ μοντέλων (Μ.Τ., πολυταινιακών Μ.Τ. και μη-ντετερμινιστικών Μ.Τ.).
- Χρονική πολυπλοκότητα μη-ντετερμινιστικών Μ.T..
- Η κλάση P.
- Η κλάση NP.
- Το θεώρημα προβολής.
- Η κλάση coNP.
- Η κλάση EXP.
- Αναγωγές και πληρότητα, η έννοια της NP-δυσκολίας.
- Το θεώρημα Cook-Levin.
- NP-πλήρεις γλώσσες.
- Ψευδοπολυωνυμικότητα και ισχυρά NP-πλήρεις γλώσσες.
Χωρική πολυπλοκότητα:
- Το θεώρημα του Savitch.
- H κλάση PSPACE.
- PSPACE πληρότητα.
- Οι κλάσεις L, NL και EXPSPACE.
- NL πληρότητα.
Θεωρήματα Ιεραρχίας:
- Το Θεώρημα Χωρικής Ιεραρχίας.
- Το Θεώρημα Χρονικής Ιεραρχίας.
Προαπαιτούμενα
Οι φοιτητές θα πρέπει να έχουν αποκτήσει εξοικείωση με την έννοια του αλγορίθμου και την ανάλυση της πολυπλοκότητάς του. Πέραν αυτού, καλό θα ήταν να έχουν στοιχειώδεις γνώσεις από τα Διακριτά Μαθηματικά, τη Λογική, τη Θεωρία Συνόλων και τη Θεωρία Γραφημάτων.
Προτεινόμενα συγγράμματα
- Michael Sipser, Εισαγωγή στην Θεωρία Υπολογισμού, Πανεπιστημιακές Εκδόσεις Κρήτης (Κωδικός βιβλίου στον Εύδοξο: 86195794)
- Harry R. Lewis, Χρήστος Παπαδημητρίου: Στοιχεία Θεωρίας Υπολογισμού, Εκδόσεις Κριτική (Κωδικός Βιβλίου στον Εύδοξο: 11776)
Βιβλιογραφία
- Christos H. Papadimitriou: Computational Complexity, Pearson publications
- Michael R. Garey, David S. Johnson: Computers and Intractability: A Guide to the Theory of NP-completeness, W. H. Freeman and Company
- Sanjeev Arora and Boaz Barak: Computational Complexity: A Modern Approach, Cambridge University Press
- John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman: Introduction to automata theory, languages, and computation, Addison-Wesley