Μάθημα : Μαθηματική Βιολογία (Χειμερινό Εξάμηνο 2024-25)

Το μάθημα Μαθηματική Βιολογία διδάσκεται στο Χειμερινό Εξάμηνο του Ακαδημαϊκού Έτους 2024-25 από τον Νίκο Γιαλελή. 

Στόχος του μαθήματος

Η παρουσίαση βασικών και πιο προωθημένων μεθόδων των Διαφορικών Εξισώσεων, Δυναμικών Συστημάτων και Εφαρμοσμένων Μαθηματικών μέσω εφαρμογών στη Βιολογία.

Υπό αυτό το πλαίσιο προαπαιτούμενα μαθήματα είναι τα εξής:

Συνήθεις Διαφορικές Εξισώσεις (βασικό), Εφαρμοσμένα Μαθηματικά (προαιρετικό) και Μερικές Διαφορικές Εξισώσεις I (προαιρετικό).

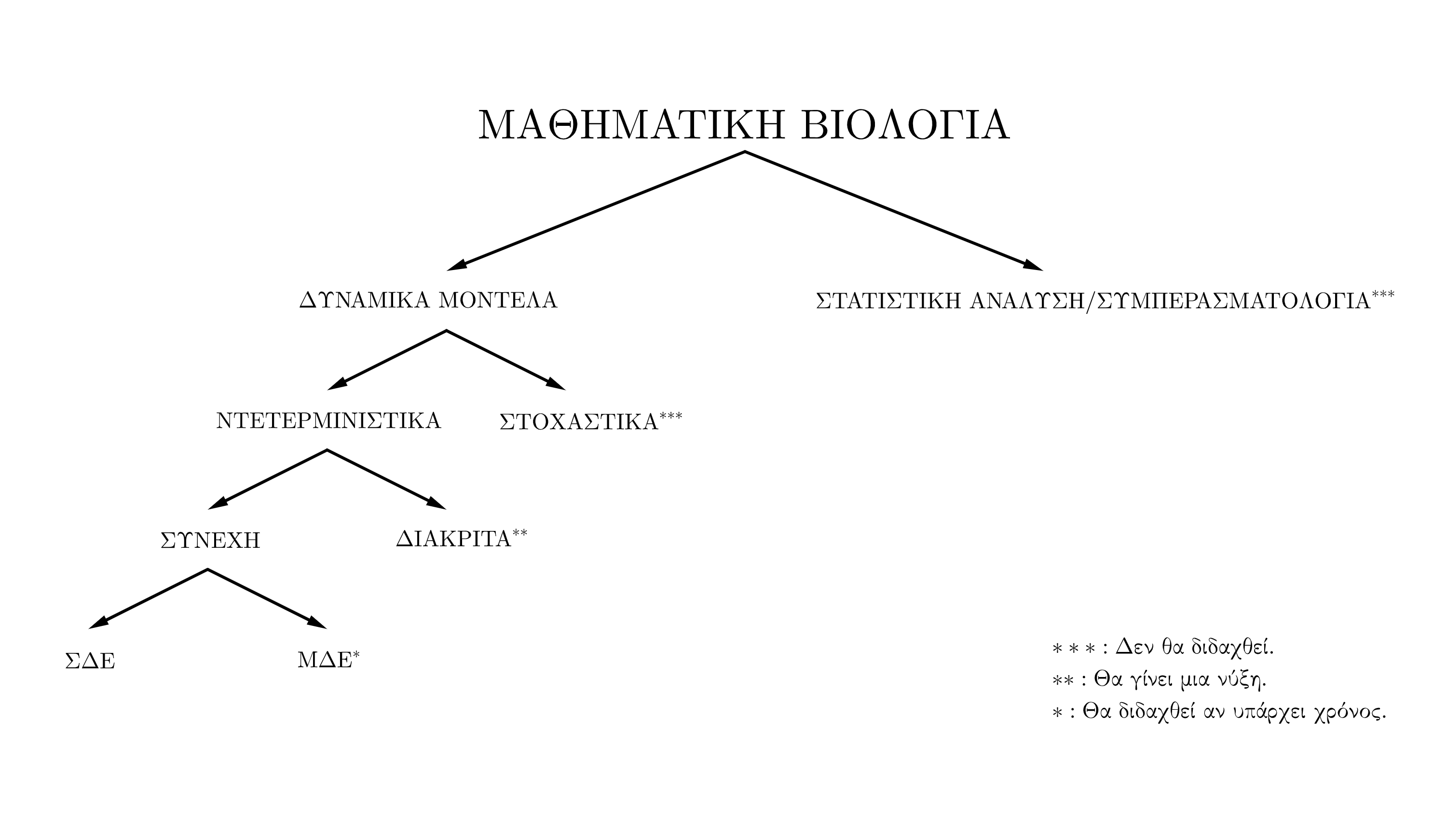
Περιεχόμενο μαθήματος

• Χρονικά μοντέλα Οικολογίας
• Χρονικά μοντέλα Επιδημιολογίας
• Βιοχημική κινητική
• Διάχυση^*
• Μηχανική Βιολογικών Ρευστών^*

Ενδεικτική Βιβλιογραφία

1. Iannelli, M., & Pugliese, A. (2015). An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka(Vol. 79). Springer.
2. Murray, J. D. (2002). Mathematical biology: I. An introduction.Springer Science & Business Media.
3. Murray, J. D. (2003) Mathematical biology II: spatial models and biomedical applications. Springer-Verlag.
4. Segel L. A. (1984) Modeling Dynamic Phenomena in Molecular and Cellular Biology, Cambridge University Press.
5. Edelstein-Keshet, L. (2005). Mathematical models in biology. Society for Industrial and Applied Mathematics.
6. Keener, J. P., & Sneyd, J. (2009). Mathematical physiology I: Cellular physiology. Springer
7. Keener, J. P., & Sneyd, J. (2009). Mathematical physiology II: Systems Physiology. Springer
8. Okubo, A., & Levin, S. A. (2001). Diffusion and ecological problems: modern perspectives.Springer Science & Business Media.
9. Κομηνέας Σ., Χαρμανδάρης Ε. (2015)  Μαθηματική Μοντελοποίηση, Αποθετήριο Ελληνικών Ακαδημαϊκών Ηλεκτρονικών Συγγραμμάτων και Βοηθημάτων Κάλλιπος. http://hdl.handle.net/11419/6325